kirchhoff’s law
Contents
Kirchhoff’s voltage law
(KVL)
According to Kirchoff’s Voltage Law (KVL), In any closed circuit or mesh, the algebraic sum of all the emf (voltage source ) and all the voltage drops will zero. This Law deals according to the principle of conservation of energy, and according to the principle of conservation of energy Net energy supplied must be Equal to Net energy consumed or Net energy consumed must be equal to Net energy supplied. This means the total amount of voltage available any circuit is the exact same as the total drop voltage in that circuit.
If you know the supply voltages in the circuit then you can find the unknown quantity in the circuit by applying the KVL., and the KVL works in 2 types of voltages – Voltage rise and voltage drop.
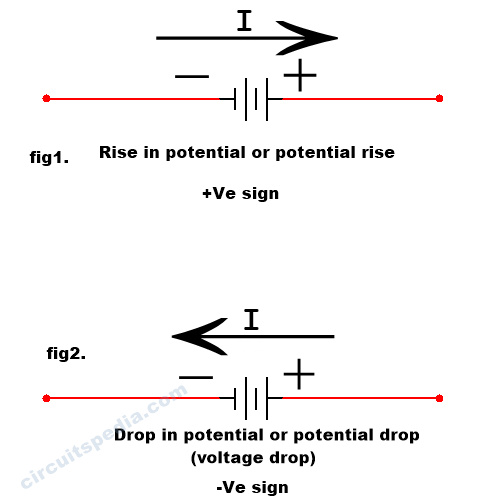
What is Rise in potential and drop-in potential?
As shown in fig1. the direction of flow of current denoted towards the higher potential to lower potential.- This is called Rise in potential or Potential rise. This is always denoted with +ve sign.
In fig 2. the direction of flow of current denoted towards lower potential to higher potential – This is called Drop in the potential or potential drop, we also called voltage drop. This is always denoted with -ve sign.
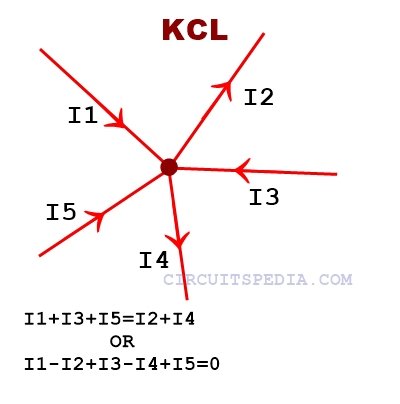
kirchhoff’s current law (KCL)
Kirchoff’s current law- According to Kirchoff’s current law the algebraic sum of all current meetings at a point or a junction will be zero. This law is based on the principle of conservation of charges. According to the principle of conservation of charges, Net charges dissipated from the junction or a point is exactly equal to the Net charge provided to the junction. This means the amount of output current is the same as the total amount of input current you provided.
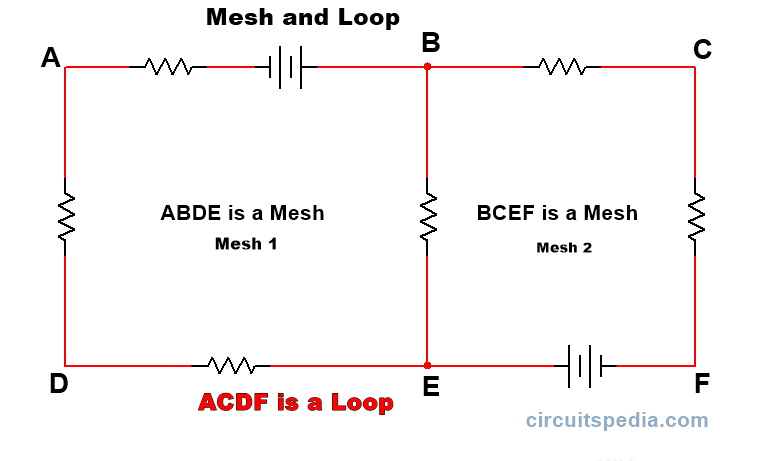
Mesh
Mesh is the closed path of an electrical circuit through which current can flow but through that close path or across the close path there is no other close path inside it.
In the given diagram ABDE can be called a Mesh and BCEF also can be called a Mesh because both is a closed path and no other closed path inside it.
Loop
A loop is a closed path of an electrical circuit through which current flow but various other closed paths contains inside it.
Difference between Loop and Mesh
A Mesh is a closed path only, no other paths contain inside a Mesh But there are various small paths that may contain in a loop. This is a difference between Mesh and Loop.
Examples
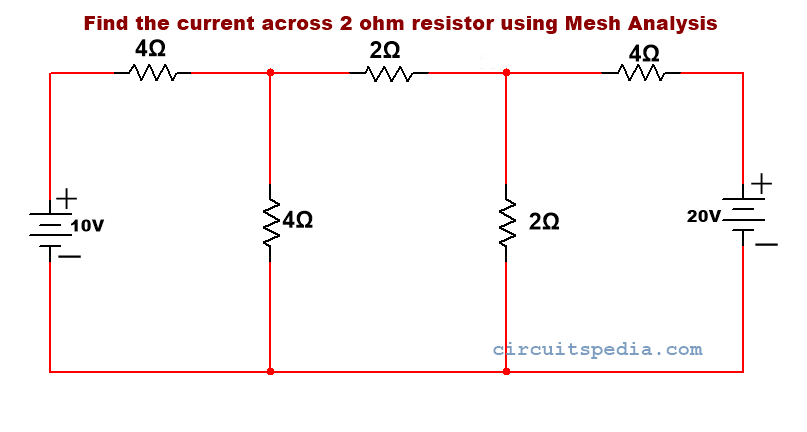
Example 1
Q1. Calculate the current through 2 Ω resistor using the Mesh analysis method.
solution-
Step 1 – Identify all meshes in the circuit
Step2 -Directions assign in all meshes. clockwise or anticlockwise as you like. But directions of all meshes are in the same direction.
Step2 -Apply KVL in each mesh and identify equations for each.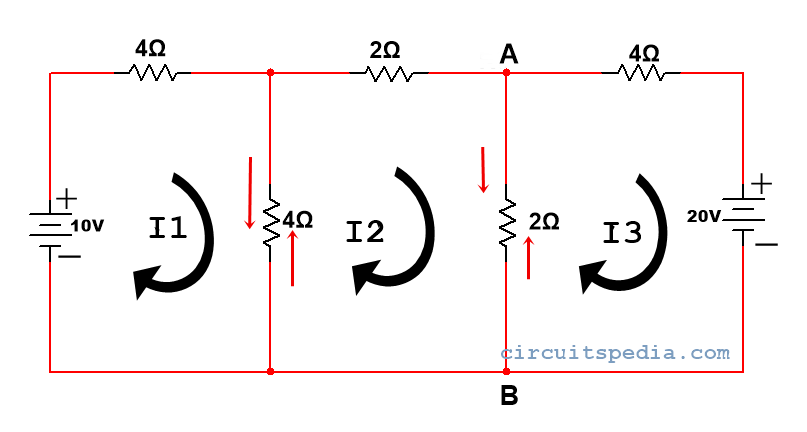
Applying KVL in mesh 1
here the direction is lower potential to higher
so, 10-I14-4(I1-I2) = 0
because current goes through a resistor, there is always a voltage drop in the resistor. so, I14 is in -ve sign. and in another 4Ω resistor, there are two directions of current, in mesh 1 from upper to lower and in mesh 2 lower to upper .so, here we write 4(I1-I2).
10-4I1-4I1-4I2=0
or, -8I1-4I2=-10—–eq1
Applying in mesh 2.
–2I2-2(I2-I3)-4(I2-I1)=0
-4I2-2I3-4I2-4I1=0
-8I2-2I3-4I1=0—–eq2
Applying KVL in mesh 3.
here the direction is higher to lower on 20v supply so,
-20-2(I3-I2)-4(I3)=0
-6I3-2I2=20—–eq3
By solving eq1 ,2 and 3
I1=1.093A
I2=-0.312A
I3=-3.43A
Now we have to find the current from 2Ω resistor, there are 2 current I2 and I3 flowing through point A and Point B.
So, IAB= I2-I3 {because here value if current I2 is greater than I3)
IAB=-0.312-(-3.43)=-3.125A
Examples based on KCL (Node analysis Method)
steps for solving the question.
Step1. Identify the principal nodes or junctions present in the network
Step2. Assign a junction potential on each junction with respect to the assign reference junction having value Vo=0V (practically grounded)
Step3. Assuming all the current in the outgoing direction from each junction (You can assume incoming current). Form KCL equations
Step4. Solve the equations to calculate the value of junction potentials
Step5. Using individual junction potentials find the value of the required electrical quantity.
Example 2
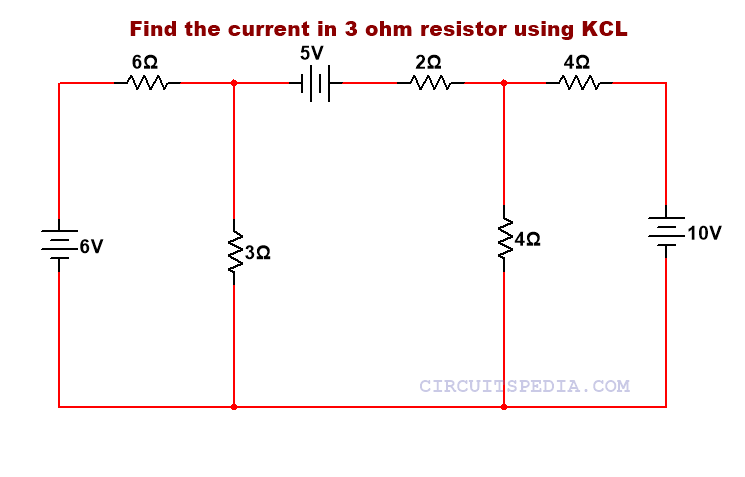
Q2. Find the current in 3Ω resistor using KCL.
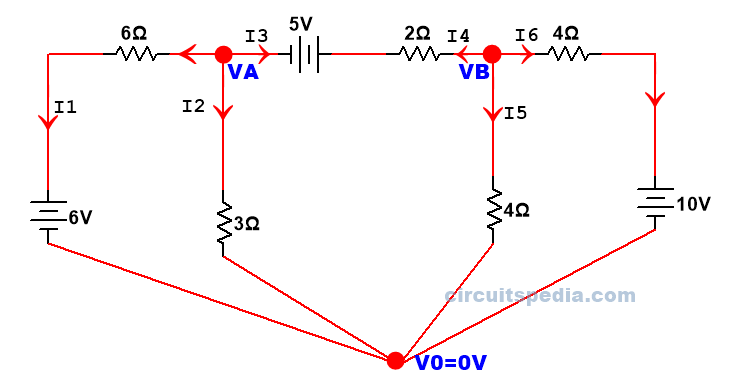
As Step 1 and step2. – Identify the principal node in the network So, I got total 2 junctions in the here. We denoted as VA and VB. and assign reference junction with V0=0V
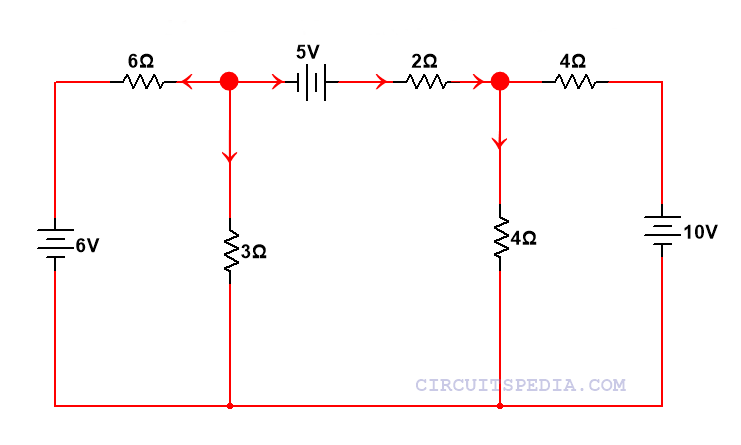
we can also see this circuit as below
Step 3. Assuming all current to outgoing direction on each junction and form the equations by apply KCL
Example 3
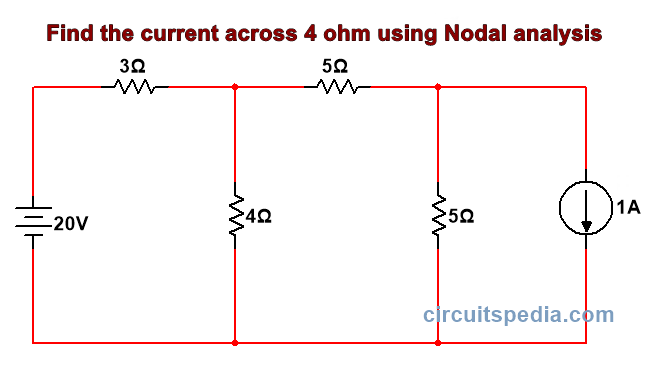
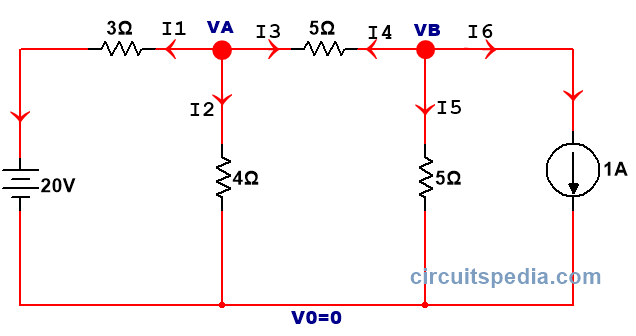
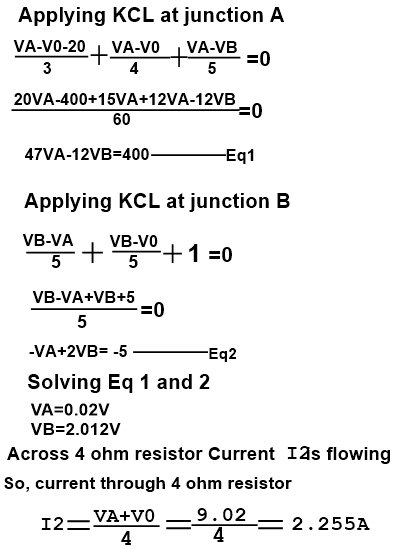
Q3. Find the current across 4Ω resistor using Nodal analysis
Solution-
Step1. Identify all junctions
Step2. Assign junction potential at each junction with respect to reference junction assign V0=0V
Step3. Assume the current flowing outgoing from each junction
Step 4. Solve the equations to calculate the value of junction potentials
Also read