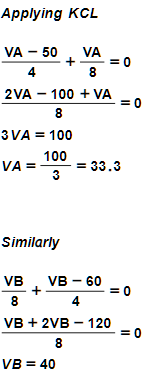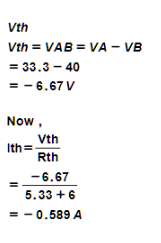Thevenin theorem
Contents
Thevenin theorem statement
Thevenin’s theorem is very important in point of view to Simplify the Network and Reduction of Network complexity in any circuit. This is also a very important theorem for Engineering and diploma students in basic Electrical.
Thevenin theorem definition
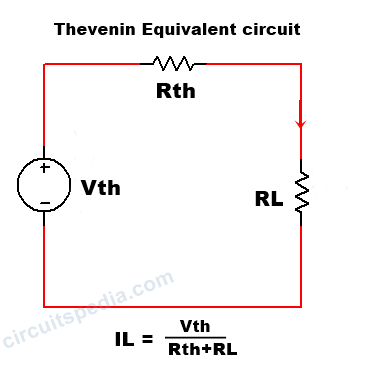
According to Thevenin’s theorem, any linear bilateral network irrespective of its complexities can be reduced into a Thevenin’s equivalent circuit having the thevenins’ open circuit voltage Vth in series with the Thevenin equivalent resistance Rth along with load resistance RL .
This theorem is named Thevenin’s theorem on the name of scientist Thevenin, he fist apply this theorem to the analysis of a circuit. By using this theorem we can reduce the complexity of any circuit network and can simplify if only two criteria are fulfilled 1st the network is linear and 2nd is bilateral. We see two elements in the simplified network 1st are Thevenin equivalent voltage Vth this is also called open-circuit voltage (Voc) , a series resistance Rth connected with this vth, this series resistance Rth is called Thevenin equivalent resistance. all of them are connected in series with a load resistance RL.
We can find the current IL which is flowing through the load resistance RL in any Thevenin equivalent circuit.
IL=Vth/Rth+RL
This identity is nothing But Ohm’s law {I=V/R}. Here RL is the load resistance which to say that finds the value in any question.
Now we go to steps that help us to solve the numerical question of Thevenin theorem. There are following steps required to solve the Thevenin’s theorem questions.
- Identify the load resistance value of RL
- Remove the load resistance and calculate the open circuit potential across the two open ends. This will be equivalent to Thevenin voltage Vth.- If I require the potential of load resistance then we need to remove the load resistance because after the removing of load resistance, there will create the Two points and at that point where we can find the potential difference, and this potential is called Thevenin equivalent Thevenin voltage. The reason behind removing the load resistance is to we need to find the voltage, If we need to find the current then I can short-circuit on that. So we remove the RL and Leave that point open and the potential difference between two points is our Vth or Voc(It is also said that open-circuit voltage).
- Again remove the load resistance and replace all active sources with their internal resistance and find Rth – If we find the equivalent resistance then there is no need of any active sources. We required only the internal resistance of those active sources.
- Calculate the equivalent resistance across the open ends. – This will we the Thevenin equivalent resistance Rth.
- Draw the Thevenin equivalent network.
- Calculate the Load current IL using this identity IL=Vth/Rth+RL
Thevenin’s theorem problems
Example 1
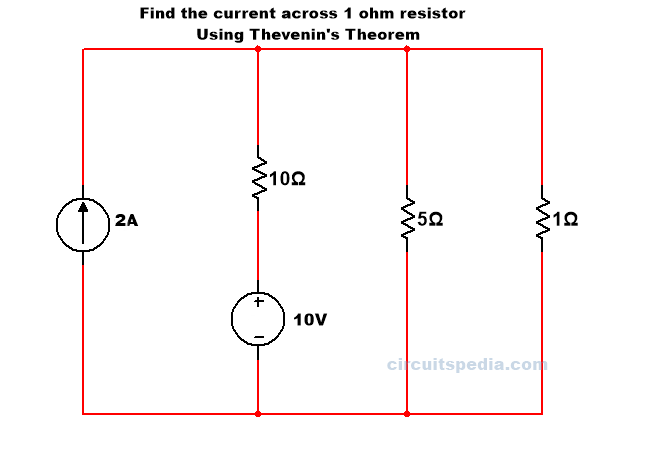
Q. Find the value of current through 1Ω Resistor in the given circuit using Thevenin’s theorem.
Solution – First we have to remember that the IL Load current is current flow across the resistor which value says to find in question. So here IL is the current of the resistor of 1Ω and this is also here the load resistor RL. In question value across which resistor asks that is Load resistor RL.
According to step 1 find the value of RL- Here Value of RL = 1Ω
In 2nd step remove the Load resistance and calculate the open circuit Vth for the two open ends.
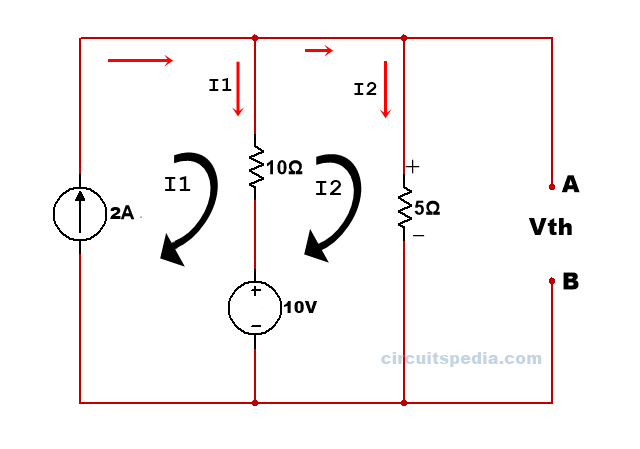
We can calculate the voltage at pint a and b using Kirchoff’s law (KCL AND KVL). so we use here KVL, first, we need a path between point a and b that completes a circuit between these. we need All elements to convert into voltage. So we have the shortest path between A and B through the 5Ω resistor. If we have the value of current across 5Ω resistor then I can calculate the voltage across 5Ω using Ohm’s law.
Applying KVL in All meshes.
I=2A
10-10(I2-I1)-5I2=0
-15I2=10I1=-10
-15I2=-10-20=-30
-15I2=-30
I2=30/15=2A
The voltage across the 5Ω resistor is V=I*R=2*5=10Ω
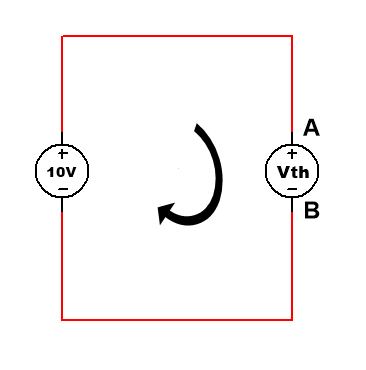
and we consider point A and b is a voltage source of Vth, then the voltage of Vth is
-Vth +10=0
Vth=10V
Now we replace all active voltage and current sources with their internal resistance
If any circuit there is internal resistance as given below
[Voltage – if not given internal resistance of voltage source in any circuit means 0Ω=short circuit
Current – α(Infinite)= Open circuit)]
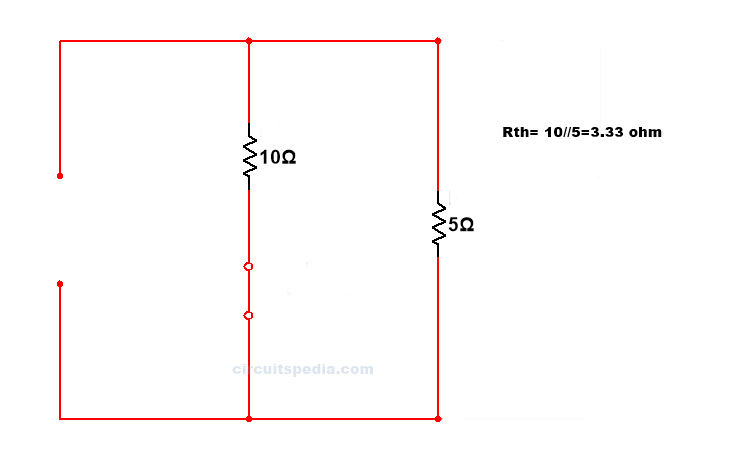
step 3 Remove again load resistance and replace all sources with their internal resistance, Then circuit will as below
Rth= 1/10+1/5 =3.33Ω
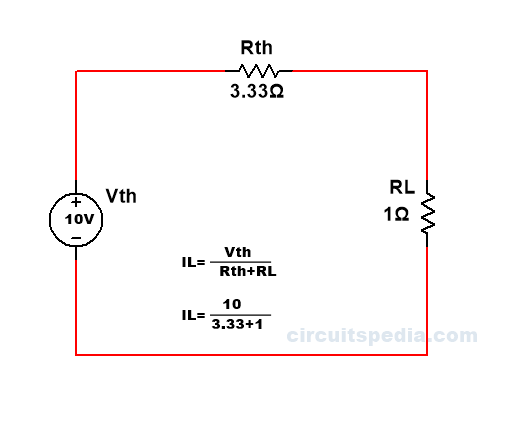
IL= Vth/Rth+RL=10/3.33+1
=2.309
Example 2
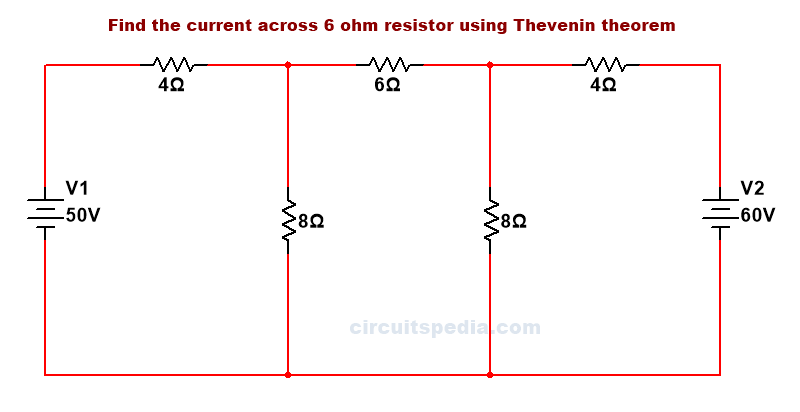
Q.2 Find the value of current across resistor 6Ω resistor using Thevenin’s Theorem.
solution –
The formula is IL= Vth/Rth+RL
RL is given in all circuits because the value of current across which resistor asked in the question, is Load resistor RL.
so Rl=6Ω
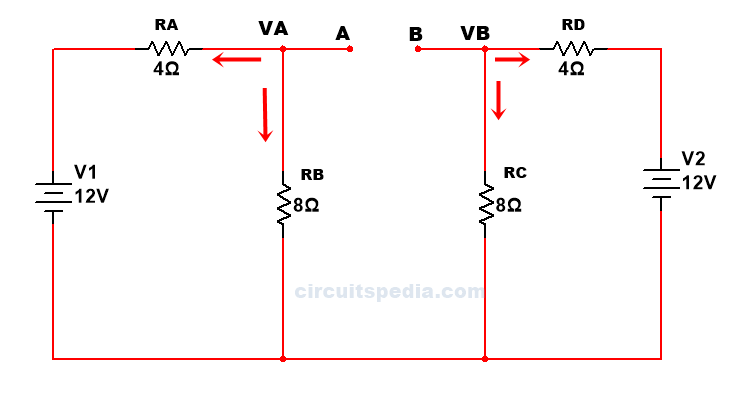
First, we remove the load resistance RL and make it open at that point.
After that replace all active sources with their internal resistance. Now, here no any internal resistance is given in sources.so, we assume that the internal resistance of all sources have 0Ω . Then sources are short circuits.
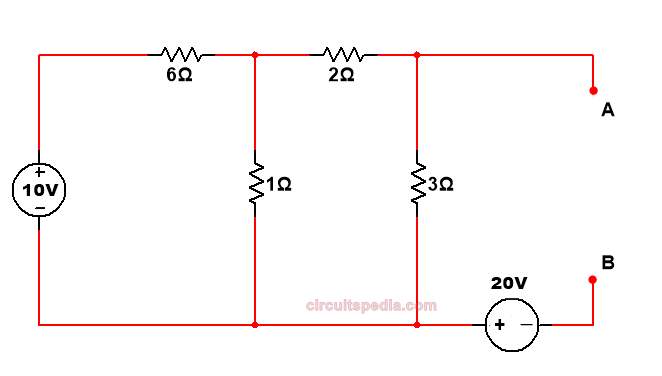
Example 3
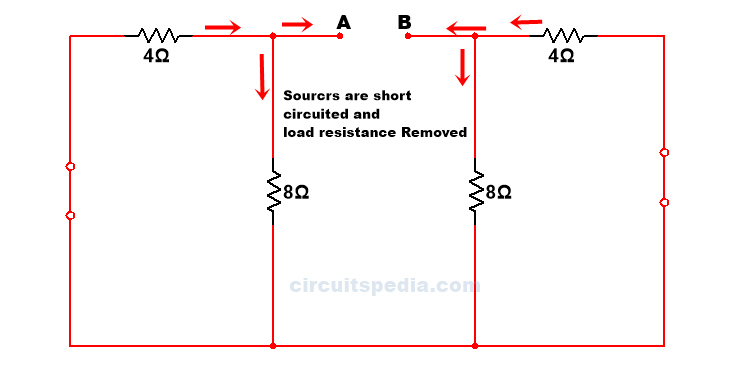
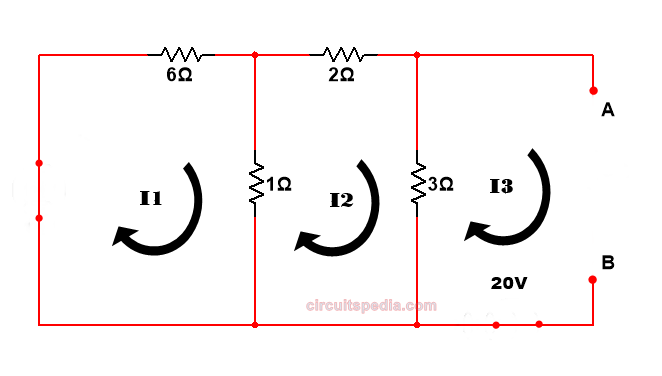
Q.3 Find the value of current across 5Ω resistor using the Thevenin’s Theorem
solution –
First, we remove the load resistor 5Ω from the circuit.
Replacing the sources with their internal resistance.
We find the current equation in all meshes using KVL
7I1-I2 =10 ——eq.1
-I1+6I2=0 ——eq 2.
by solving eq1 and 2 ——-eq.1
I1=1.46341
i2=0.243
Applying KVL in mesh 3
-3(I3-I2)-Vth-20=0
-I3+3I1-Vth+20=0
3I2-Vth+20=0
I3=0 (because this mesh is open)
3(0.2434)+20=Vth
Vth=20.73170v
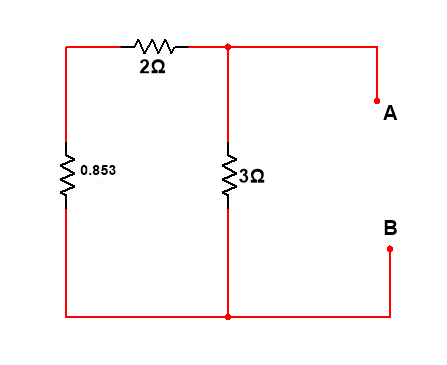
1//6=0.857
Rth = 2.857//3=1.4637
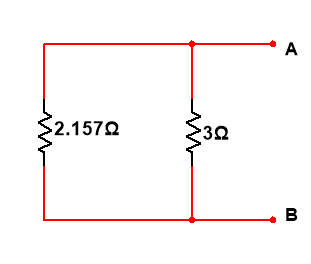
Draw the Thevenin equivalent circuit and calculate the value of current using ohm’s law
1.4637+5
=3.20756A Ans.
Also read
-
Kirchoff’s law (kcl, kvl)
-
Norton’s Theorem
-
How capacitor block dc current
-
LOGIC GATES
-
Semiconductor P-N Diode | P-N Junction