Number system

Introduction

A number system is a mathematical framework used to represent and express numbers using specific symbols or digits in a structured manner. Each number system follows a set of rules that define how numbers are written and interpreted. Number systems are essential for performing mathematical operations such as addition, subtraction, multiplication, and division.

Number systems are also referred to as position-weighted systems because the value of each digit depends on its position within the number and the base of the system.

Key Concepts of Number Systems

• If the base of a number system is ‘r’, the number of different symbols used in the system is also ‘r’.
• The largest digit value in a system with base ‘r’ is always r – 1.

Types of Number Systems

Number systems are classified based on their base values. The four most commonly used number systems are:

1. Binary Number System (Base-2)
2. Octal Number System (Base-8)
3. Decimal Number System (Base-10)
4. Hexadecimal Number System (Base-16)

Binary Number System (Base-2)

The binary number system is the foundation of digital electronics and computing. It consists of only two digits: 0 and 1. Each digit position represents a power of 2.

Key Characteristics:

• The maximum digit in the binary system is calculated as r – 1, which is 2 – 1 = 1.
• A binary number consists of a series of 0s and 1s, such as 101011.
• Each position of a digit in a binary number corresponds to a power of 2.

Example:

Binary number 1011 represents:

Conversion: Decimal to Binary

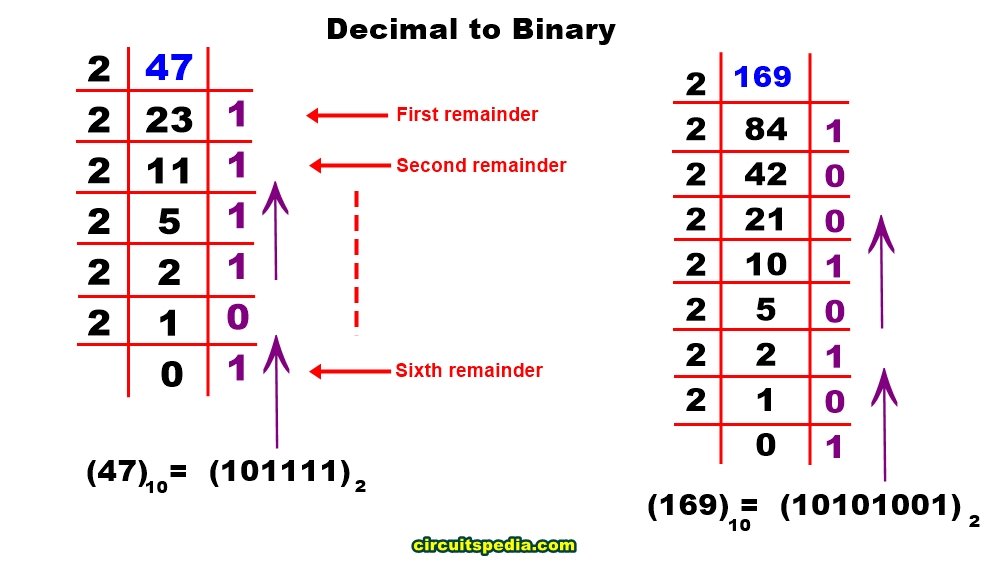
To convert a decimal number into binary, follow these steps:

For the Integer Part:

1. Divide the integer by 2.
2. Record the remainder.
3. Repeat the process with the quotient until it becomes zero.
4. The binary equivalent is the reversed order of remainders.

For the Fractional Part:

1. Multiply the decimal fraction by 2.
2. Record the integer part.
3. Repeat the process with the remaining decimal part until it becomes zero or reaches the desired precision.
4. The binary equivalent is read in the same order.

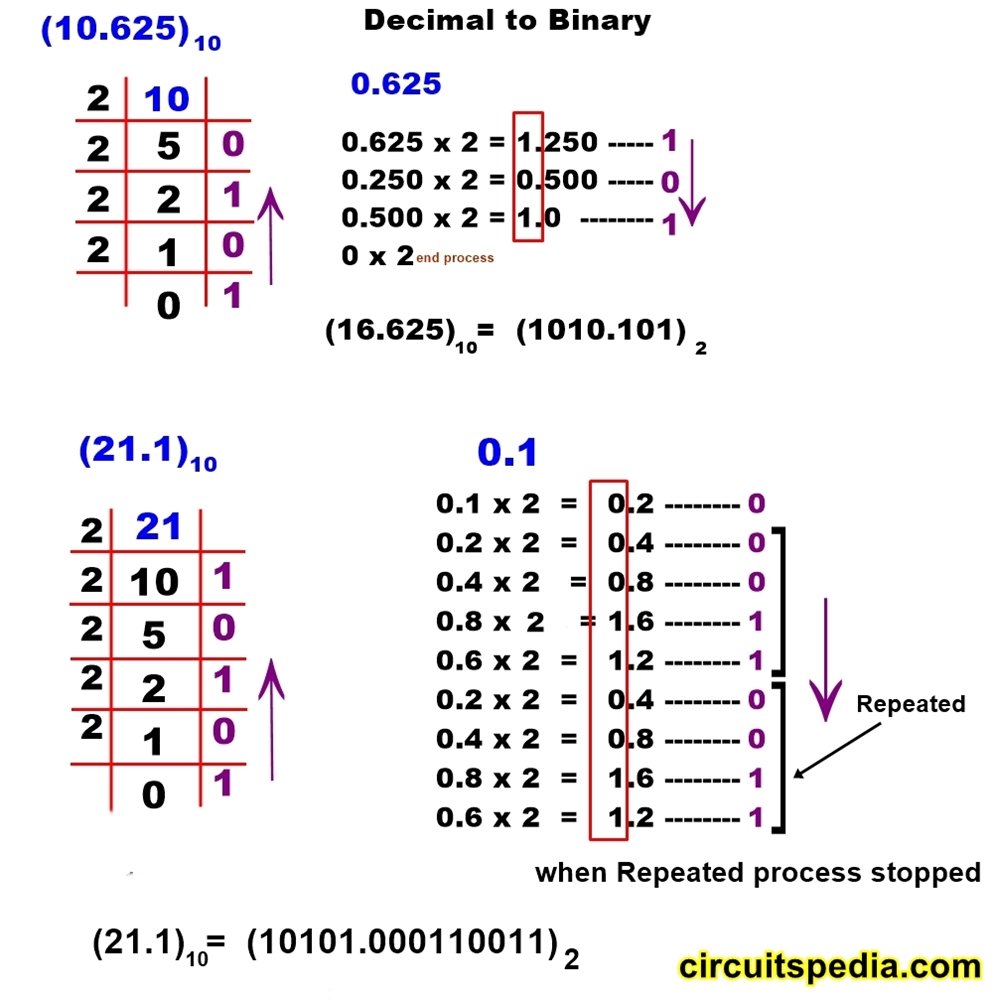
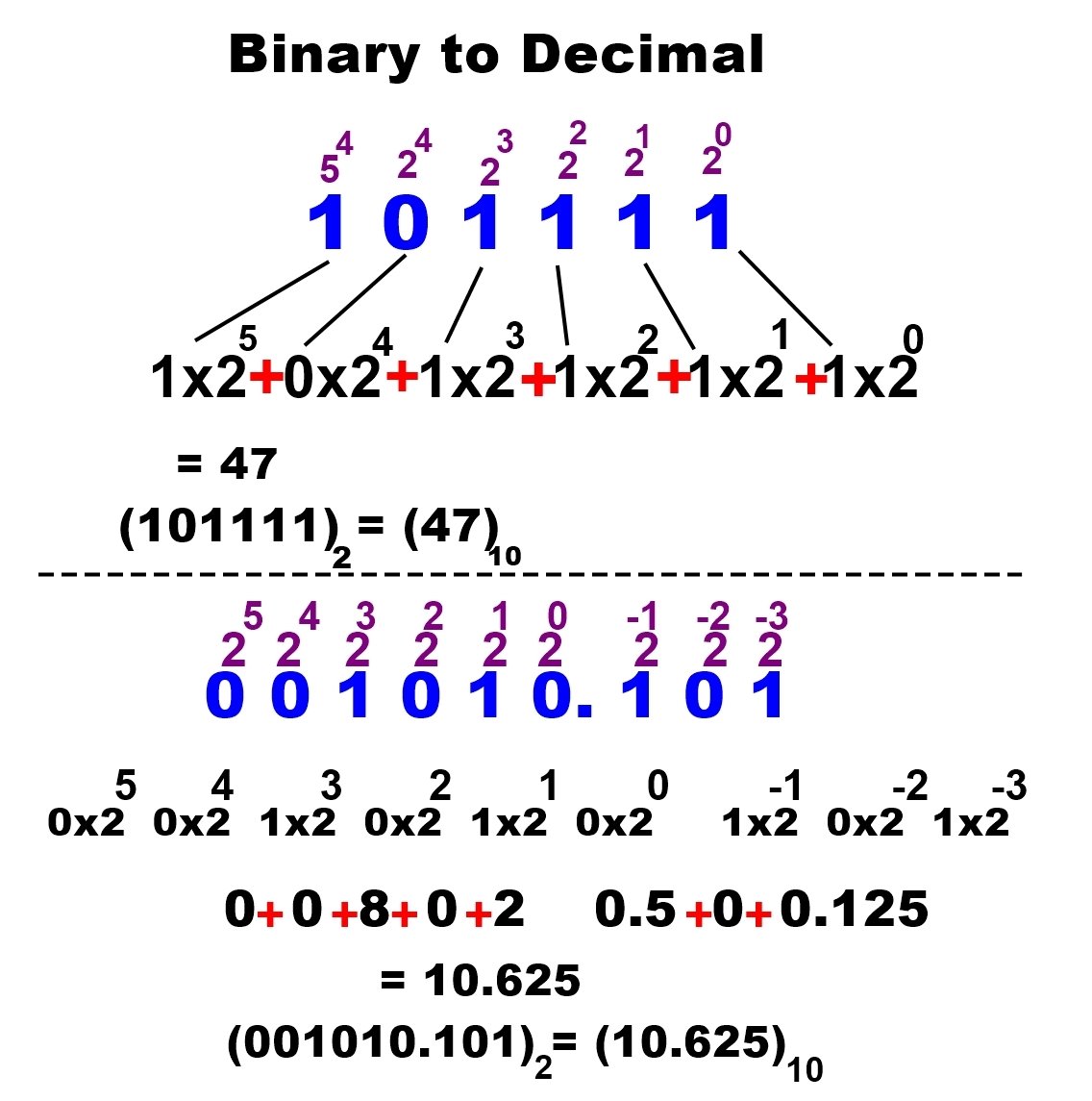
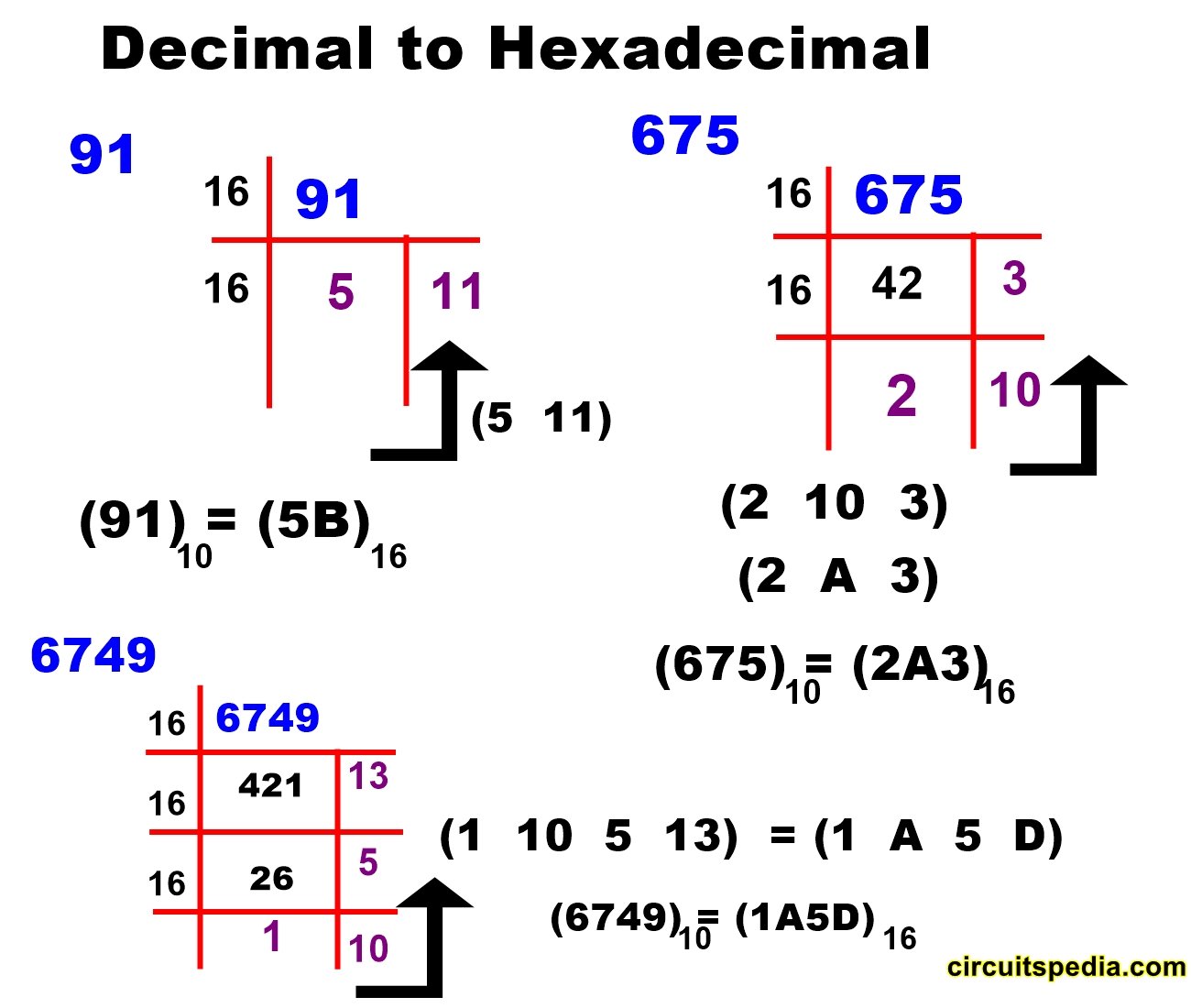
How to Convert 10.625 (Decimal) to Binary (Base-2)

To convert 10.625 (decimal) to binary, we need to separately convert the integer part (10) and the fractional part (0.625).

Step 1: Convert the Integer Part (10) to Binary

We repeatedly divide by 2 and record the quotients and remainders.

Step	Division by 2	Quotient	Remainder
1	10 ÷ 2	5	0
2	5 ÷ 2	2	1
3	2 ÷ 2	1	0
4	1 ÷ 2	0	1

Binary equivalent of 10 (reading remainders from bottom to top) → 1010_₂

Step 2: Convert the Fractional Part (0.625) to Binary

We repeatedly multiply by 2 and record the integer part.

Step	Multiplication by 2	Integer Part	Fractional Part
1	0.625 × 2	1	0.25
2	0.25 × 2	0	0.5
3	0.5 × 2	1	0.0

Binary equivalent of 0.625 → .101₂

---

Step 3: Combine Both Parts

Now, we combine the integer and fractional binary results:

10.625₁₀=1010.101₂

10.625 {10} = 1010.101 {2}

Final Answer: 10.625 (decimal) = 1010.101 (binary) 

Octal Number System

The Octal Number System is a base-8 number system, meaning it uses eight unique digits: 0, 1, 2, 3, 4, 5, 6, and 7. The prefix “OCT” stands for eight, indicating that this system is based on powers of 8.

Each digit in an octal number represents a power of 8, similar to how the decimal system (base-10) represents powers of 10. The highest single-digit value in the octal system is 7, as the value of the base minus one is (8 – 1) = 7.

Characteristics of the Octal Number System

• Uses digits from 0 to 7.

• Base = 8, meaning each place value is a power of 8.

• Commonly used in digital electronics and computing as a shorthand for binary numbers.

• Efficient representation for microcontrollers and embedded systems.

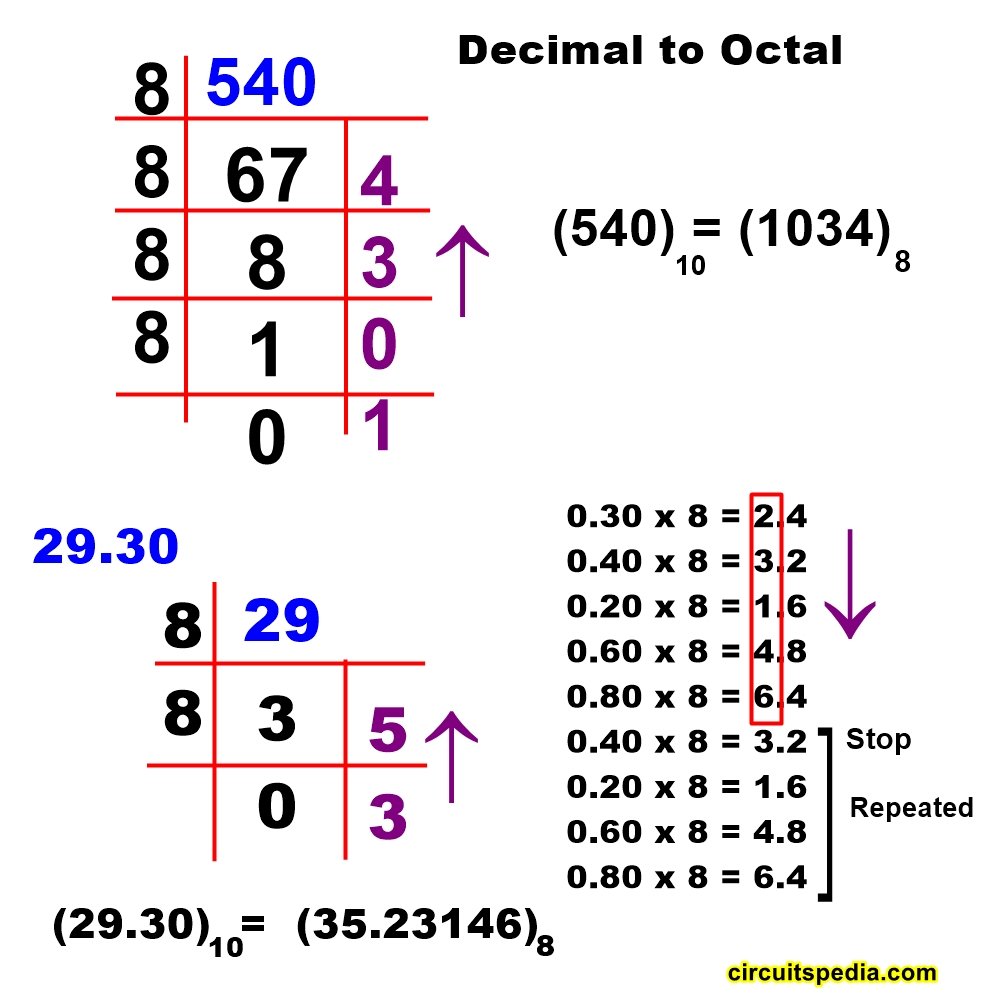
To convert a decimal number (base-10) to an octal number (base-8), we follow these steps:

Step 1: Divide the Number by 8

We continuously divide the decimal number by 8 and record the quotient and remainder.

Step 2: Read the Remainders in Reverse Order

Reading from bottom to top, the octal equivalent of 540₁₀ is:

540₁₀=1034₈540{10} = 1034 {8}540_10​=1034₈​​

Applications of the Octal Number System

1. Used in Digital Electronics – Efficiently represents large binary numbers in a compact form.
2. Used in Shift Registers – Common in microcontrollers and embedded systems.
3. Shorthand for Binary Numbers – Since one octal digit corresponds to three binary digits, it simplifies binary calculations.
4. File Permissions in Unix/Linux – File permissions are often represented in octal notation (e.g., 755).

Decimal to Octal Conversion

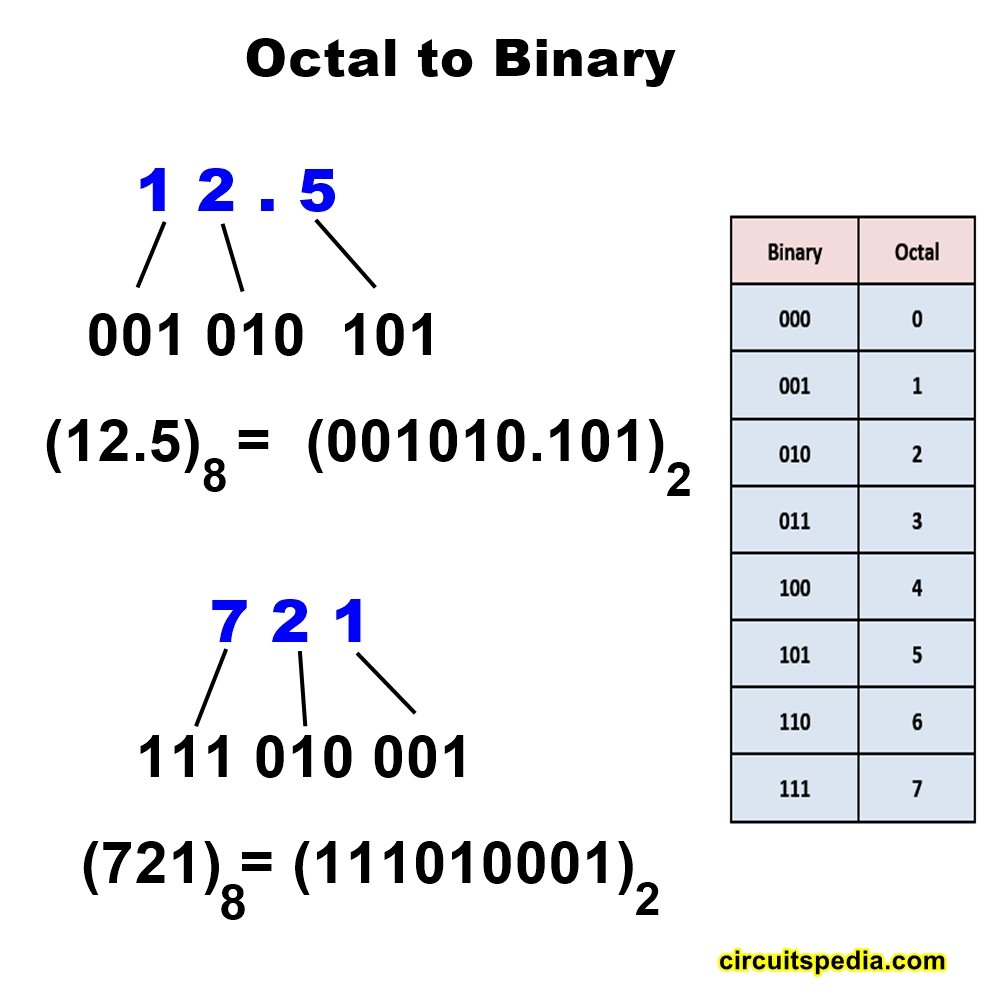
Octal to binary conversion

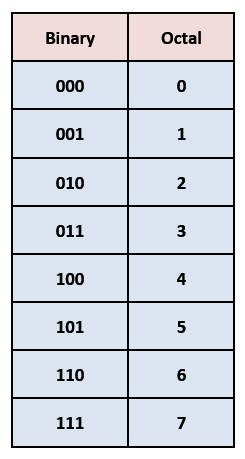
As we know 8 = (2)3
So, each digit in the octal number system will be replaced by its equivalent binary using three bits. Hence direct conversion of octal to binary is possible.
(12.5)8 = (001010.101)2

Binary to octal

For binary to octal conversion, we will form a group of three bits starting from the origin, and then we will write the decimal equivalent of each group.
(001010.101)2 = (12.5)1

Decimal number

The numbers are represented or expressed with base 10 in the decimal number system. In this system, 10 digits (0 – 9) are used to represent a number. This is also called the base-10 number system. Each digit has a value in a decimal number according to its value, this is called place value. The place value increased 10 times the position of the umber when moving right to left.

Binary to decimal conversion

 

Hexadecimal number

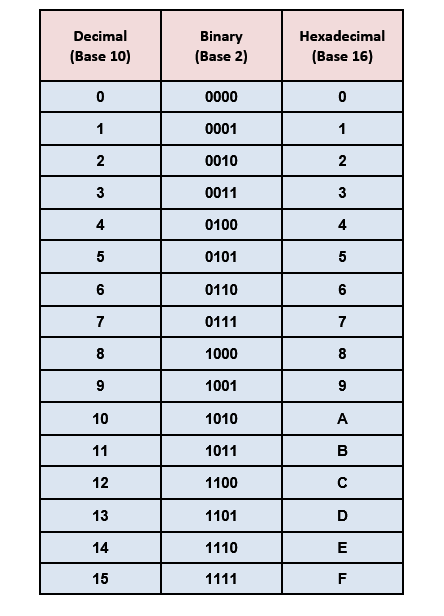
A hexadecimal number is also called a base-16 number or sometimes called Hex. This is the combination of Hexa (6) and decimal (10). A hexadecimal number is a numbering technique to represent any number in the form of base 16. in The hexadecimal system uses 0-9 and then uses A to F There are only 16 symbols or digits used to represent the hexadecimal number. These 16 symbols and digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. A is equal to 10, B is equal to 11, and so on till F is equal to 16.
The hexadecimal number system is used to represent large-value binary numbers. The hex number is much easier to read or express than binary and decimal.

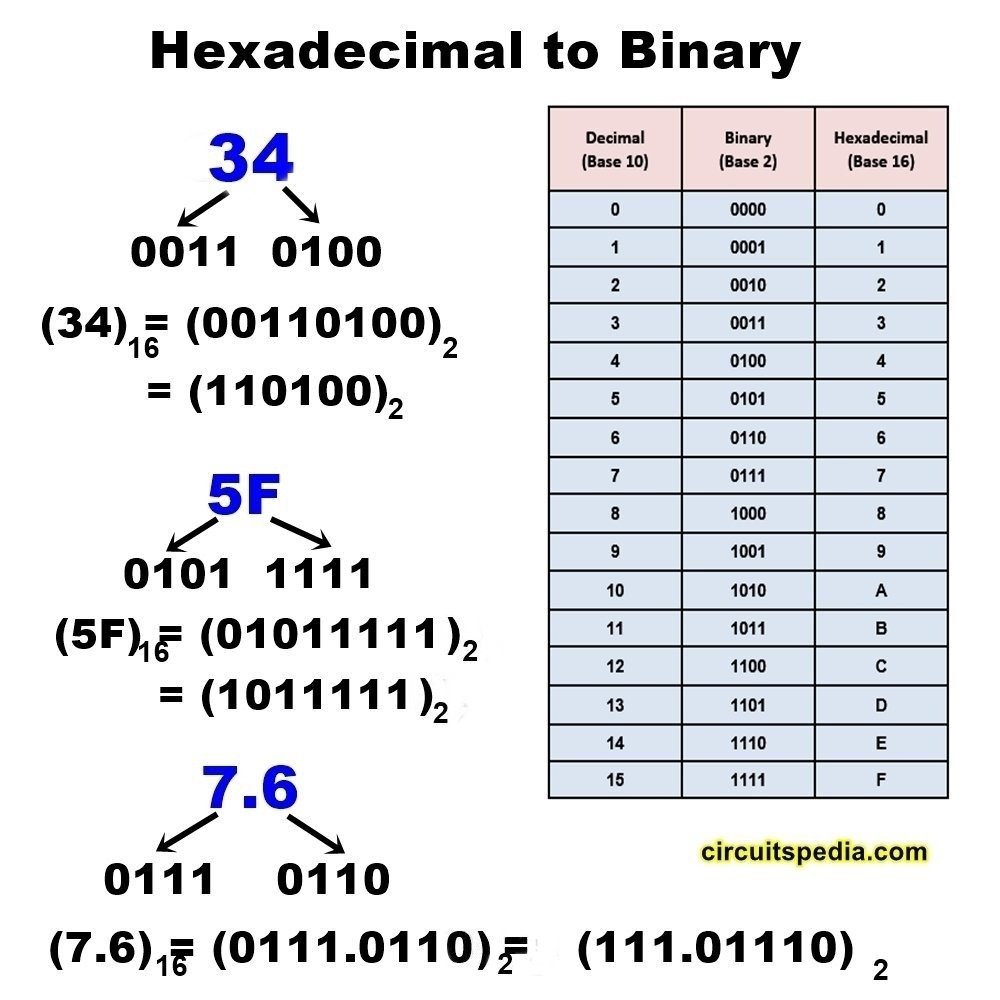
Steps for converting binary to hexadecimal

1. Make groups of 4 digits from right to left (In fractional-left to right after the point). If the numbers are not in groups of 4 digits, then add an extra 0 left end (also right end in fractional numbers) to make groups of 4
2. Find the equivalent hexadecimal number for each group
3. Write the hexadecimal of each group as per group’s order

Hexadecimal to Decimal

How to Convert Hexadecimal to Decimal (Step by Step)

The Hexadecimal (Base-16) number system uses 16 symbols:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F, where:

• A = 10, B = 11, C = 12, D = 13, E = 14, F = 15 in decimal.

To convert a hexadecimal number to decimal, follow these steps:

Step-by-Step Conversion Method

1. Write down the hexadecimal number.

2. Identify the positional values (each position is a power of 16, starting from the rightmost digit).

3. Multiply each digit by 16 raised to its position value.

4. Add up all the results to get the decimal equivalent.

Example: Convert 2F3 (Hex) to Decimal

We will convert 2F3₁₆ to Decimal (Base-10).

Step 1: Assign Positional Values

2F316= (2 × 16²) + (F × 16¹) + (3 × 16⁰)

Step 2: Convert Hex Digits to Decimal

• 2 remains 2
• F = 15 in decimal
• 3 remains 3

Step 3: Multiply Each Digit by 16 Raised to Its Position

(2×16²)+(15×16¹)+(3×16⁰)

 (2×256)+(15×16)+(3×1)

 512+240+3=755

Final Answer: 2F3_₁₆ = 755_₁₀

Another Example: Convert B7A (Hex) to Decimal

B7A16=(B×16²)+(7×16¹)+(A×16⁰)

Convert hex to decimal values:

• B = 11
• A = 10
• 7 remains 7

Multiply each by powers of 16:

(11×16²)+(7×16¹)+(10×16⁰)

 =(11×256)+(7×16)+(10×1) =2816+112+10

= 29382816 + 112 + 10 = 2938

Final Answer: B7A₁₆ = 2938_₁₀

Summary of Conversion Steps

1. Write the hex number and assign positional values.
2. Convert hex digits to decimal equivalents (A-F → 10-15).
3. Multiply each digit by 16 raised to its position.
4. Add all the values together to get the final decimal number.

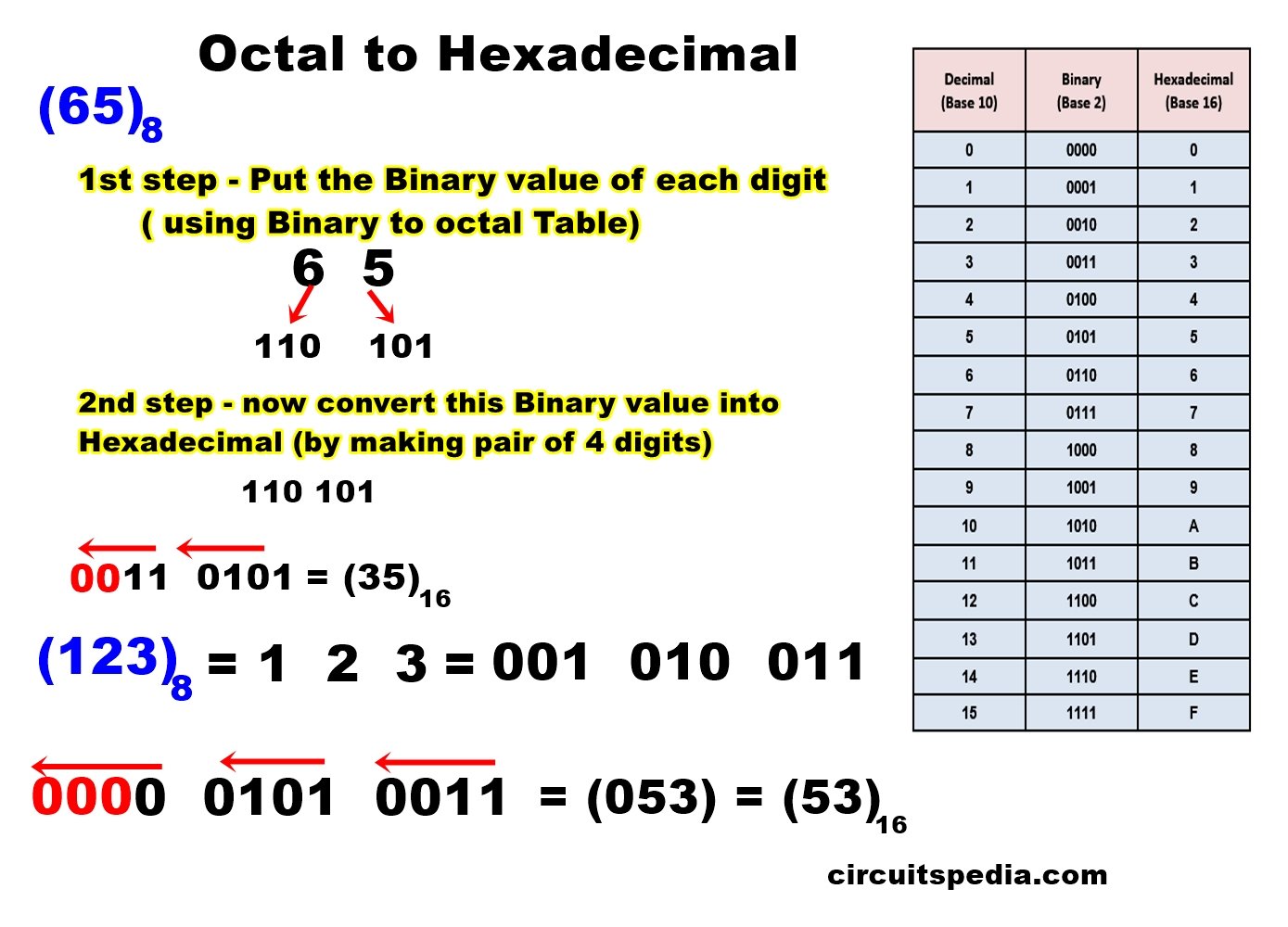
Steps for converting Octal to hexadecimal

1. Place the value of binary from octal number of each digit using binary to octal table.
2. Now, make pairs of 4 binary digits. If more digits, then place an extra 0 on the right end of the numbers to make pairs of 4.
3. Place the value of Hexa of each pair using the binary to hexadecimal Table.

Converting decimal to hexadecimal

Decimal to Hexadecimal 

Uses of Hex Codes

• Many error codes and other values of codes are represented by hexadecimal on the computer. Errors and any warning codes on the blue screen in computers are generally represented in the hex format. Hex codes are shorter than binary and decimal, so the programmer uses this.
• In the programming of web designing a specific color code is also represented in HTML format using the Hex codes. For example, the hex value FF0000 defines the color red.
• Programmers use Hex codes in the coding of a program because of the value of Hex codes are shorter than the decimal or binary.

 

Also read

• Kirchoff Theorem

• How capacitor block dc current

• Arduino Remote control AC Dimmer

• Automatic Night Lamp Using LDR